Lab Report on Molecular Mass Determination by Boiling Point Elevation Method

1. Aim and Abstract:

To determine the molar mass, M of an unknown compound by boiling point elevation method.

When a non-volatile solute is added to a pure solvent, the resultant solution would have a higher boiling point than the pure solution. The boiling point of a solution is a colligative property (Atkins 2010: 170 – 171) and is dependent on the concentration of the solute in the solution but not on what the solute and solvent are. This boiling point can be measured by an ebullioscope.

T1 – T2 = ΔT = Kbm     where ΔT is the magnitude of the boiling point elevation

                                                Kb is the ebullioscopic constant of the solvent

                                                m is the molality of the solution

Using the equation above, the molality of the solution can be determined. Consequently, the molar mass and nature of the unknown sample can be determined.

2. Results and Calculations:

1. Unknown code: 2        

2. Volume of ethanol used: 25.00cm3

3. Weight of test tube with unknown (w1): 18.7925g

4. Weight of empty test tube (w2): 15.5564g

5. Weight of unknown (w1 – w2): 3.2361g

6. Temperature of boiling ethanol: 77.0 °C

7. Temperature of boiling unknown in ethanol: 79.0 °C

From the results above, ∆T = T1 – T2 = (352.15 – 350.15) K = 2.0 K

Mass of ethanol solvent = density × volume

= 0.785gcm-3 × 25cm3

= 19.63g

= 1.963 x 10-2 kg

Given that the magnitude of the boiling point elevation ∆T is:

T1 – T2 = ∆T = Kbm             where m = molality of the solution

                                                           Kb = ebullioscopic constant of solvent

ΔT = Kb m

∆T = Kb ×

     =

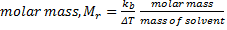
Mr = 1.22 / 2.0 x 3.2361/0.01963Therefore, Mr of unknown sample, code 2 = 100.6 gmol-1 (4 sig. fig.)

3. Discussion:

Assumptions made during the experiment

During the experiment, the solution of ethanol provided is assumed to be free from other impurities as the presence of impurities will increase the boiling point of ethanol. It is important for the actual boiling point of ethanol to be accurately determined as the value would be used in the calculation of the molar mass of the unknown sample.

The experimentally determined value of the boiling point of ethanol was 77.0°C which could be considered to be fairly accurate, considering that the literature value of the boiling point was 78.5°C and the thermometer used during the experiment had an accuracy of ± 0.05°C.

During the course of the whole experiment, the concentration of ethanol was constant, assuming that no evaporation and reaction with the unknown substance had occurred. This is because the mass of the solvent is required in the calculations to find the molar mass of the unknown substance and it is dependent on the volume of ethanol used.

Raoult’s Law on vapor pressure[2]

Boiling at a specific temperature indicates that the vapor pressure of a liquid is equal to the external pressure. In terms of intermolecular interactions, the boiling point represents the point at which the liquid molecules possess enough thermal energy to overcome the various intermolecular attractions binding the molecules as liquid (e.g. dipole-dipole attraction, instantaneous-dipole induced-dipole attractions, and hydrogen bonds) and therefore incur a phase change into the next phase (gas).

By applying Raoult’s Law, the extent of boiling point elevation when a solute is added to a solvent can be understood. This understanding is based on the assumption that a non-volatile solute is added to a dilute and ideal solution.

Raoult’s Law states that the vapor pressure of an ideal solution is dependent on the vapor pressure of each chemical component and the mole fraction of the component present in the solution can be expressed as:

       pA = xA • pA*  where pA* refers to the vapor pressure of the pure liquid A,

                                            xA refers to the mole fraction of A and

                                          pA refers to the vapor pressure of A when another substance is present in the liquid.

In any solution, the mole fraction of a component decreases with additional components. Therefore, when the unknown sample was added into the ethanol solvent, the number of components in the mixture increased, hence the mole fraction of ethanol decreases.

As a result, the vapor pressure of the ethanol solvent decreases because the less volatile solute molecules present at the solution surface layer partially blocks the evaporation of the solvent molecules.

Also, when a solute dissolves in a solvent, the initial solvent-solvent interaction is broken and replaced by a stronger solvent-solute interaction. Hence, more energy is required to overcome the stronger forces of attraction between the solute and solvent, accounting for a rise in boiling point when a solute is added to a solvent. 

 

Boiling point elevation diagram(left)[3]. When a nonvolatile solute is dissolved in a pure solvent to produce a solution, the original boiling point of the solvent, Tb, is raised to a new value, Tb’.

Nature of unknown sample

Raoult’s Law is most applicable for ideal solutions.  An ideal solution is defined as a solution containing components of uniform intermolecular forces of attraction; if the molecules of 2 components of a solution have the equal tendency to escape the liquid surface, the solution is said to be ideal; there will not be an enthalpy change when two ideal solutions are mixed. It is observed that there is a 2.0°C increase in the boiling temperature of the ethanol solvent, when the unknown is added. This means that the resultant solution formed aftering mixing was not ideal – the non-volatile unknown sample does not possess the same molecular size and intermolecular forces of attraction as ethanol.

When a non-volatile solute, such as a salt, is added to a pure solvent, the boiling point of the resultant solution will be raised above that of the pure solvent. The magnitude of the boiling point elevation ∆T can be written as:

         ΔT = Kb · m · i        where ΔT is the magnitude of the boiling point elevation,

                                                        Kb is the ebullioscopic constant of the solvent,

                                                        m is the molality of the solution and

                                                         i is the number of particles formed by a compound in solution

Boiling point elevation is a colligative property and is dependent on the number of solute particles present and not on their chemical identity. The Van’t Hoff factor, i, of the unknown sample is 1 – the unknown does not ionize – which is why it is excluded during calculations. From this, we can postulate that the unknown sample does not ionize in ethanol.

Furthermore, with its ability to dissolve in ethanol, a polar solvent, the unknown is either polar or ionic in nature since the hypothesis of bonding states that for dissolution to take place, the solvent-solute interaction formed has to be greater or similar in strength with the polar solvent-solvent and solute-solute interactions.

It is possible to determine the molecular mass of the unknown sample through boiling point elevation method as the unknown substance is less volatile than the ethanol solvent. This is evident as, at room temperature, ethanol is a volatile solvent while the sample is a solid.

*

Experimental set-up for the determination of the molecular mass by Ebullioscopic method (CM1131 Laboratory Manual, 2010)

Experimental Techniques

In the setup of the experiment, the glass tubing serves as a mean for the gas molecules present in the boiling tube to escape. It is to ensure that a closed rigid environment is not established during this experiment as boiling does not happen in a closed rigid environment. In a closed environment, while the vapor pressure of the liquid is rising, the extra vapor that evaporates increases the pressure upon the liquid. The vapor pressure thus never reaches the same value as the environmental pressure, because both values are increasing as a result of heating. This problem does not arise in the open environment (i.e. in the presence of the glass tubing) because the vapor that evaporates is free to disperse; therefore, it is able to establish pressure equality between the vapor and the surroundings and boiling can occur.

Besides providing an open environment so that boiling can occur, the glass tubing also allow for gaseous molecules to escape into the environment. This prevents a dangerous build-up of pressure within the boiling tube which may cause the glassware to crack or shatter.

Also, the glass tubing acts as a condenser. With its cool internal surface, it will cause gaseous ethanol molecules – which have a low boiling point at around 780C – to condense and prevent them from escaping. This is important as the number of ethanol molecules directly affects the mass of the solution and thus, the molality of the solution.

Also, the experiment was carried out in a hot water bath. This allows the temperature of the solution to increase gradually, which in turn allows for the boiling points of ethanol with and without the unknown sample to be more accurately determined. To ensure even distribution of heat, a magnetic stirrer was added.

Reliability of the results

The molality of a solute is referred to as the number of moles of solute per kilogram of solvent. Therefore, the mass of solvent used is crucial as it is involved in the calculation of the molecular mass of the unknown sample. Any spills or vaporization causing the loss of solvent will directly cause a deviation of the empirical molecular mass from its literature value. Thus, any steps involving the transfer of ethanol has to be handled with great care, as ethanol is a volatile liquid.

The boiling tube is cooled in an ice bath before the stopper was carefully removed. This is to lower the temperature of the solution so that boiling will stop and the ethanol molecules will not escape. This allows for the accurate determination of the molality of the solution.

Also the temperature of the water bath must not be too high. If the temperature of the water bath is much higher than the boiling point of ethanol, the ethanol sample will be vaporized excessively, leading to a loss in accuracy of results.

The first bubbles observed from the capillary do not necessarily suggest boiling. It may be due to the escape of dissolved air in ethanol. A steady stream of bubbles must be observed to ascertain the boiling point.

Besides observing the steady stream of bubbles originating from the capillary, the boiling point of ethanol can be confirmed and made more reliable with other additional observations. Firstly, droplets of ethanol will condense on the internal walls of the boiling tube and thus, indicate that boiling is taking place. Also, ethanol will condense and form droplets in the glass tubing. Additionally, during boiling, the temperature of the solution remains constant. When all four phenomenon are observed, it can be safely concluded that the temperature recorded is indeed the boiling point of the solution.

5. Conclusion:

The molecular mass of the unknown sample (Code 2) is determined to be 100.6 gmol-1 by the boiling point elevation method. The boiling point elevation of solutions is a common phenomenon observed when a solute is dissolved in a pure solvent.

6. Exercises:

Q1. What causes the boiling point elevation and what is the meaning of “molality”?

Boiling occurs when the vapor pressure is equal to the external pressure. Boiling point elevation happens when a non-volatile solute is dissolved in a pure solvent.

In any solution, the mole fraction of a component decreases with additional components. Therefore, when the unknown sample was added into the ethanol solvent, the number of components in the mixture increased, hence the mole fraction of ethanol decreases. As a result, according to Raoult’s law, the vapor pressure of the ethanol solvent decrease and more energy is required for the solvent molecules to escape the solution, thus a higher boiling point.

The less volatile solute molecules present at the solution surface layer partially blocks the evaporation of the solvent molecules. Also, when a solute dissolves in a solvent, the initial solvent-solvent interaction is broken and replaced by a stronger solvent-solute interaction. Hence, more energy is required to overcome the stronger forces of attraction between the solute and solvent, accounting for a rise in boiling point when a solute is added to a solvent.

Molality is referred to as the number of moles of solute particles present in a kilogram of solvent. It is useful when the properties of the solvent, rather than the properties of the solute, are being studied. It has units of mol kg-1.

 

As compared to molarity (M), which is defined to be number of moles of a solute (mol) dissolved per volume of solvent (L), molality calculations is independent of temperature since it is calculated based on the number of moles of solute as well as mass of solvent and both are temperature independent. Molarity (M) on the other hand, is temperature dependent since its calculation involves the use of volume of solution which is temperature dependent. However, the disadvantage to molality is that the density information must be known to determine the amount of the mixture.

Q2. Why does the concept of colligative properties apply only to dilute solutions?

Colligative properties refer to properties which depend only on the number of solute particles present and not their chemical identity. Examples of such properties are boiling point elevation, freezing point depression and lowering of vapour pressure and osmotic pressure.

A dilute solution is one that has a small quantity of solute dissolved in a relatively large amount of solvent. The solute particles are relatively further apart from each other in the solution, creating an ideal environment such that the solute particles experience little intermolecular interaction. This assumption thus works well for many dilute solutions, especially solutions of molecular compounds.

However, as the concentrations increase there will be stronger solute-solute interactions and the nature of the solute particles become important. There are more solute particles and these particles are closer together and intermolecular interactions are no longer negligible. The properties will no longer be colligative as it is affected by the identity of the solute too. Thus, colligative properties do not apply to concentrated solutions.  

Q3. What are the limitations of the molar mass determination by boiling point elevation method?

The limitations to the molar mass determination through the use of the boiling point elevation method are listed below:

i) Only non-volatile solutes should be used in the experiment. This is due to the fact that if a volatile solute is used, the solute would contribute to the vapour pressure and hence the boiling point determined for the solution would be inaccurate.

ii) The degree of the dissociation of the solute has to be taken into account i.e. whether the solute is an electrolyte or not. If the solute is an electrolyte, the electrolyte would dissolve to give ions and the ion concentration would be much higher than that of the solute.

      For example, XY (s) → X+ (aq) + Y- (aq)

Hence, the boiling point would be increased to a greater extent when dissolving an electrolyte as compared to dissolving a non-electrolyte for the same solute concentration. Therefore, the solute chosen may cause inaccuracy in the results.

iii) Another limitation would be that the solution used has to be a dilute one in order to create an ideal environment such that the solute-solute interactions are minimized. This dilution is to prevent the interactions from affect the concentration of the solution. In a concentrated solution, the solute-solute interactions present are significant hence it will affect the accuracy of the molecular mass calculated at the end of the experiment.

iv) A limitation would be the usage of a mercury-in-glass thermometer to measure the boiling point of the solvent. Firstly, it is difficult to determine the accurate boiling point of the solvent as it can only be read to the nearest degree Celsius. Also, it can only be used to measure the boiling points of solvents with boiling points lower than 110°C as the thermometer can only measure limited temperatures ranging from -10°C to 110°C. There may be fluctuations in the temperature readings hence it is hard to determine the exact boiling point of the solution. Furthermore, a slight difference in temperature can result in an inaccuracy of the calculated molar mass.

Q4. What is the molality (m) of a solution prepared by dissolving 2.5g of NaCl in 550.0g of H2O whose density is 0.997g cm-3?

Molality (m) = (no. of moles of solute) ÷ (mass of the solvent in kg)

= (mass ÷ molar mass) ÷ (mass of solvent in g ÷ 1000)

= (2.5 ÷ 58.44) ÷ (550 ÷ 1000)

                            = 0.07778 molkg-1 (4 sig. fig.)

Q5. A 0.750 M solution of H2SO4 in water has a density of 1.046g/mL at 20°C. What is the concentration of this solution in molality?

Mass of H2SO4 present in water = 1.046g/mL × 1000mL

= 1.046 kg

Molality = (no. of moles of solute) ÷ (mass of the solvent in kg)

= 0.750 ÷ 1.046

                            = 0.7170 molkg-1 (4 sig. fig.)

7. References:

1. Boiling point as a colligative property: Atkins Physical Chemistry, Peter Atkins and Julio de Paula, 2010, pg 170-171

2. Raoult’s Law: http://en.wikipedia.org/wiki/Raoult's_law

3. Boiling point elevation method: http://www.cbu.edu/~rprice/lectures/evap1.html#bpe

4. Boiling point elevation diagram: http://en.wikipedia.org/wiki/File:Freezing_point_depression_

and_boiling_point_elevation.png